July’s Tip

The author was introduced to Mulligan Mechanics in late eighties, while attending one of Dr. Mulligan’s presentations, “Common Sense Mechanics.” After attending numerous Dr. Mulligan’s lectures, the author embraced his philosophy of biomechanics and applied it to his everyday practice.

Dr. Thomas F. Mulligan (1933 – 2023) was a renown orthodontist, mentor and educator from Phoenix, Arizona.  He authored and published 25 articles, lectured in 32 countries, and authored and published three books, “Common Sense Mechanics in Everyday Orthodontics.” Dr. Mulligan simplified biomechanics and deftly explained Forces, Moments, Moment to force ratio, Center bend, Off-center bends, and Static Equilibrium.

Do not memorize, understand – Dr. T. Mulligan

Static Equilibrium

Requirements for Static Equilibrium: The sum of all horizontal, vertical forces and moments around common point equals ZERO.

The following image explains the basic principles of the moments and forces in Mulligan mechanics. The author and some of his course attendees had difficulties at the beginning to embrace his philosophy.

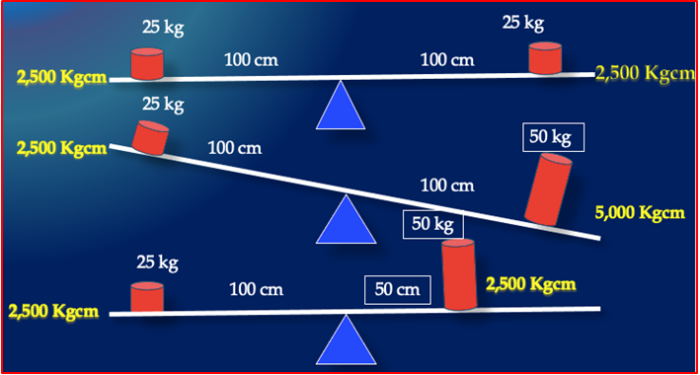
Let us analyze the Static Equilibrium on the teeter-totter:

First example on the image: two children, the same weight – 25 kg decided to play on the teeter-totter.  Both sat down at the end of the board – 100 cm from the fulcrum and the teeter-totter was in Static Equilibrium. After the activation (one side pushing off the ground), each side had a potential of 2,500 kg/cm (25×100 – force x distance) of downward moment of the force.

Second example on the image: the child on the right side left, and their older sibling came to play. He sat down, and the board went down on his side. Why did this happen?  Both children sit 100 cm from the fulcrum, however one on the left produces 2,500 kg/cm (25×100), the other on the right side 5,000 kg/cm (50×100 – force x distance) moment of the force. The Static Equilibrium was violated.

Third example on the image: The child on the right side studied physics in the high school, thus he decided to move closer to the fulcrum, and low and behold, they were in Static Equilibrium.  Why did this happen? The smaller child produced 2,500 kg/cm of moment of the force and the larger child the same – 2,500 kg/cm moment of the force (50×50 – force x distance), ergo, they achieved the Static Equilibrium

What did we glean from this example?

The smaller weight (force) and larger distance (wire)

Equals to 

The larger weight (force) and smaller distance (wire}
When we can not move the boulder with our hands (short distance), 
we take a long crowbar (long distance) to move it.  
The same strength, only longer distance